9. 源收敛诊断与加速

蒙卡临界计算采用裂变源迭代法，裂变源分布的收敛速度取决于系统占优比。对于高占优比 的系统（如全堆、乏燃料池），裂变源收敛可能需要数百代甚至上千代，从而导致大量计算 时间耗费在对统计结果无直接贡献的非活跃代。

9.1. 香农熵和渐进相对熵统计

RMC源收敛模块提供香农熵（Shannon Entropy）统计功能，定性地反映裂变源分布的收敛 趋势，帮助用户选择合理的非活跃代中子数。

香农熵的定义为：

\[H(S) = - \sum_{i} S(i) \log _2 \left( S(i) \right)\]

其中，\(S(i)\) 为第 \(i\) 个网格的裂变源份额。

RMC源收敛模块也提供渐进相对熵（Progressive Relative Entropy, PRE）统计功能。与香农熵功能类似， PRE可以定性地反映裂变源分布的收敛趋势，帮助用户选择合理的非活跃代中子数。

相对熵的定义为：

\[D(S||Y) = \sum_{i=1}^B S(i) \log _2 \left( \frac{S(i)}{Y(i)} \right)\]

其中， \(S\) 和 \(Y\) 都是裂变源分布，\(S(i)\) 和 \(Y(i)\) 是第 \(i\) 个网格的裂变源份额。 \(D(S||Y)\) 始终非负， 且当 \(S = Y\) 时， \(D(S||Y) = 0\) 。

香农熵能够表征源分布的无序程度，相对熵则表征两个源分布之间的偏离程度。相对熵越大，偏离程度越大，两个源分布间的相似度越小。 相对熵可能出现无穷大的情况，因此更好地表征两个源分布之间偏离程度的量是渐进相对熵PRE。PRE的定义为：

\[PRE(j) = D(S^{(1)} || 0.5 \times (S^{(1)} + S^{(j)})) + D(S^{(j)} || 0.5 \times (S^{(1)} + S^{(j)}))\]

其中，\(S^{(j)}\) 为第 \(j\) 个迭代步的裂变源分布。

香农熵或渐进相对熵通过以下输入卡定义：

SeMesh [Scope = < xNum yNum zNum >]
[Bound = <xMin xMax yMin yMax zMin zMax>]
[PRE = <flag>]
[Output = <flag>]

其中，

  • SeMesh为香农熵网格输入卡的关键词。
  • Scope选项卡指定香农熵网格在x、y、z方向的网格划分数量。xNum、 yNum、zNum为正整数。
  • Bound选项卡指定香农熵网格在x、y、z方向的边界范围。若在Scope选项 卡中指定某个方向的网格划分数量为-1，则默认网格边界为（-∞，+∞），此时 Bound选项卡中相应方向的边界不产生实际意义。注意，用户应保证网格范 围能够覆盖中子跟踪区域，否则会造成香农熵的统计结果错误。
  • PRE选项卡指定是否计算渐进相对熵。当PRE = 1时，计算渐进相对熵； 当PRE = 0时，不计算渐进相对熵（默认值）。注意， 程序只能计算香农熵或渐进相对熵，不能同时既计算香浓熵，也计算渐进相对熵。
  • Output选项卡指定是否输出网格中的中子源份额。 当Output = 0（默认值）时，不输出中子源份额； 当Output = 1时，输出每代的中子源份额到.Info.h5文件中的 convergence/source数据组中，每代数据集以代数命名。

9.2. 裂变源分布泛函展开系数统计

RMC源收敛模块提供统计泛函展开系数以表征裂变源分布形状的功能， 定性地反映裂变源分布形状随迭代步的变化情况， 帮助用户选择合理的非活跃代中子数。

该功能通过以下输入卡定义：

FET [Axis = <x y z>]
[Bound = <x_boundary_min x_boundary_max y_boundary_min y_boundary_max z_boundary_min z_boundary_max>]

其中，

  • FET为该功能输入卡的关键词。
  • Axis指定裂变源分布形状的坐标轴。程序只允许从笛卡尔坐标系的x、y、z 三种坐标轴方向上分别使用泛函展开系数表征裂变源分布形状。 例如，若需要x和z方向的泛函展开系数以表征裂变源分布形状， 需要指定Axis = 1 0 1。
  • Bound选项卡指定裂变源分布形状在三个方向的边界范围。 该边界范围需要大于所有中子可能发生裂变反应的位置， 在此基础上越小越好。 注意，boundary_min < boundary_max。 当不需要统计某个方向时，相关的数值可以任意。 例如，若需要x和z方向的泛函展开系数以表征裂变源分布形状， 可以指定Bound = -300 300 0 0 0 300。

需要说明的是，该选项不兼容裂变源收敛加速方法（渐进维兰德、渐进超历史方法）。

9.3. 裂变矩阵统计

RMC源收敛模块还提供裂变矩阵（Fission Matrix）统计功能。基于裂变矩阵，可以诊断蒙 卡低抽样（undersampling），并计算占优比。除了使用裂变矩阵计算占优比以外，RMC还支 持基于误差传递矩阵的占优比计算方法，目前版本暂不提供。

裂变矩阵的定义为：裂变矩阵F中的每个元素 \(F_{ij}\) 表示区域 \(j\) 中出生的中子在区域 \(i\) 中产生裂变中子的几率。

\[F_{ij} = \frac {\int _{Vi} dr \int _{Vj} dr' f(r'\rightarrow r) s_0 (r') } {\int _{Vj} dr' s_0 (r')}\]

裂变矩阵统计卡的输入方式与香农熵统计卡类似：

FmMesh [Scope = < xNum yNum zNum >]
[Bound = <xMin xMax yMin yMax zMin zMax>]

其中，

  • FmMesh为裂变矩阵网格输入卡的关键词。
  • Scope选项卡指定香农熵网格在x、y、z方向的网格划分数量。xNum、 yNum、zNum为正整数。裂变矩阵规模为 (xNum*yNum*zNum)2，过细的网格划分可能降低计算效率。
  • Bound选项卡指定香农熵网格在x、y、z方向的边界范围。若在Scope选项 卡中指定某个方向的网格划分数量为-1，则默认网格边界为（-∞，+∞），此时 Bound选项卡中相应方向的边界不产生实际意义。注意，用户应保证网格 范围能够覆盖中子跟踪区域，否则会造成裂变矩阵的统计结果错误。

9.4. 源收敛加速

RMC使用渐近超历史方法和渐近维兰德方法加速源收敛，减少非活跃代代数。目前版 本只提供渐近超历史加速方法。

源收敛加速功能的输入卡为：

AcceFsc [Factor = <f(1) p(1) f(2) p(2) …f(n) p(n)>]
        [AutoFactor = <inactive_cycle>]

其中，

  • AcceFsc为香农熵网格输入卡的关键词。
  • Factor选项卡和AutoFactor选项卡用来指定渐近超历史加速方法的参数， 后面将单独予以讨论。

9.4.1. Factor选项卡

Factor选项卡用于自定义加速参数。输入卡中的f(i)称为加速因子，p(i)称为加速周期， 其含义是：在最初的p(1)代，使用加速因子f(1)；在接下来的p(2)代，使用加速因子 f(2)；依此类推。这里不详细介绍渐近超历史加速方法的原理，仅对加速因子和加速周期 这两个参数介绍如下：

加速因子f(i)越大，加速效果越明显，但统计涨落也可能越大。用户需要定义的是一组 渐近递减的加速因子{f(i)}，譬如“16 → 8 → 4 → 2”。注意，加速因子不宜过大 （建议小于20），否则可能造成不稳定。

加速周期p(i >1)一般设置为5-10代。第一个加速周期p(1)通常设置得较大，因为它所对 应的加速因子最大，起主要的加速效果。

渐近超历史加速方法作用于最初的个非活跃代，它所产生的加速效果大致相当于未使用加速 时的个非活跃代。例如，某个全堆临界计算在未使用加速时需要大约200个非活跃代，通过 使用“factor = 16 10 8 5 4 5 2 5”加速最初的10+5+5+5=25个非活跃代，即可达到基本相 当的收敛效果。

9.4.2. AutoFactor选项卡

作为Factor选项卡的替代功能，RMC程序提供了自动生成源收敛加速参数的 AutoFactor选项卡。对于普通用户，推荐使用AutoFactor选项卡来代替 Factor选项卡中的自定义输入。在该选项卡中，用户指定未使用加速方法时的非 活跃代代数inactive_cycle，程序内部将自动生成渐近超历史方法的参数序列。 假设未使用加速方法时的非活跃代代数为N，那么使用AutoFactor选项卡后的所需 非活跃代数约为：

\[N' = \frac {N}{16} + 15\]

例如，某全堆计算需要300代收敛，那么使用自动源收敛加速之后，所需的非活跃代可设 置为：\(N' = \frac {300}{16} + 15 \approx 35\)。若AutoFactor选项卡中 指定的非活跃代代数N小于30，程序将关闭源收敛加速功能。

9.4.3. 源收敛加速的注意事项

使用源收敛加速方法，应当在临界计算模块的PowerIter输入卡中使用合理的配套参数，包括：

1）在Keff0选项卡中指定合理的初始有效增殖系数，使其接近真实Keff。

2）在Population选项卡中指定足够大的每代粒子数。对于全堆临界计算，建议每 代粒子数大于100,000。

3）在Population选项卡中指定合理的非活跃代代数。非活跃代代数应当大于等于 源收敛加速代数。

9.5. 源收敛模块输入示例

9.5.1. OECD基准题源收敛加速

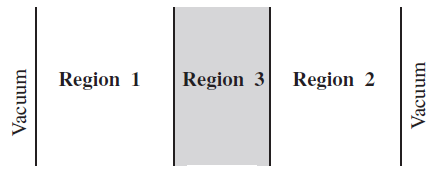
../_images/source_convergence.png

图9.1 OECD蒙卡源收敛基准题

图9.1 描述的是OECD蒙卡源收敛问题研究的一个基准题。 该基准题是由3块1维平板组成的弱 耦合系统，两侧为20cm厚的燃料区，中间为30cm水层。初始源位置位于左侧燃料区中心， 常规源迭代收敛所需的非活跃代约为1000代。通过RMC源收敛加速方法，非活跃代可减少 至100代以内。在 示例9.1 的源收敛模块中， 指定了香农熵网格数量为70，宽度为1.0cm。 该算例需要模拟的粒子数较多，推荐使用并行机完成计算。


示例9.1 OECD蒙卡源收敛输入
///// OECD MC convergence benchmark 3 . SHE Ding 2012-09-12 /////
UNIVERSE 0
cell 1 1 & -2 mat = 1
cell 2 2 & -3 mat = 2
cell 3 3 & -4 mat = 1
cell 4 -1 : 4 void = 1

SURFACE
surf 1 px 0
surf 2 px 20
surf 3 px 50
surf 4 px 70

MATERIAL
mat 1 9.9487E-02
      92235.30c 7.6864E-05
      92238.30c 6.8303E-04
      8016.30c 3.7258E-02
      1001.30c 5.9347E-02
      7014.30c 2.1220E-03
mat 2 1.0006E-01
      1001.30c 6.6706E-02
      8016.30c 3.3353E-02

CRITICALITY
PowerIter population = 500000 100 1000
InitSrc point = 10 0 0

Tally
Celltally 1 type = 1 cell = 1 3

CONVERGENCE
SeMesh Scope = 70 -1 -1 Bound = 0 70 0 1 0 1
FmMesh Scope = 70 -1 -1 Bound = 0 70 0 1 0 1
AcceFsc Autofactor = 1000

9.5.2. Hoogenboom全堆基准题源收敛加速

示例9.2 描述的是Hoogenboom蒙卡全堆基准题。常规源迭代收敛所需的非活跃代约为250代， 通过使用自动源收敛加速参数，非活跃代代数设置为35代。在源收敛输入模块中，定义了 建立在组件上的香农熵网格（21×21），用于帮助用户诊断源收敛趋势。该算例需要模拟的 粒子数较多，推荐使用并行机完成计算。


示例9.2 Hoogenboom蒙卡全堆基准题输入
// same model as previous

CONVERGENCE
SeMesh Scope = 21 21 1 Bound = -224.91 224.91 -224.91 224.91 -229 223
AcceFsc Autofactor = 250